变分法在氦原子基态能计算中的应用张朝阳的物理课解析屏蔽库伦势

在量子力学的研究中，氦原子作为一个双电子系统，其基态能量的精确计算一直是理论物理学中的一个重要问题。由于氦原子中的两个电子相互作用，使得传统的量子力学方法难以直接应用。变分法作为一种近似方法，在此类问题的解决中显示出其独特的优势。本文将围绕如何使用变分法计算氦原子基态能，并结合《张朝阳的物理课》中的屏蔽库伦势概念，进行深入探讨。

1. 氦原子基态能的挑战

氦原子由两个电子和一个原子核组成，其哈密顿量为：

\[ H = \frac{\hbar^2}{2m}\nabla_1^2 \frac{\hbar^2}{2m}\nabla_2^2 \frac{2e^2}{4\pi\epsilon_0 r_1} \frac{2e^2}{4\pi\epsilon_0 r_2} \frac{e^2}{4\pi\epsilon_0 r_{12}} \]

其中，\( r_1 \) 和 \( r_2 \) 分别是两个电子与原子核的距离，\( r_{12} \) 是两电子之间的距离。直接求解这个哈密顿量的本征值是非常困难的，因为电子间的相互作用项 \( \frac{e^2}{4\pi\epsilon_0 r_{12}} \) 是非线性的。

2. 变分法的基本原理

变分法是一种通过选择一个试探波函数，并优化其参数以最小化能量期望值的方法。试探波函数通常包含可调参数，通过调整这些参数，使得能量期望值最小，从而得到系统的近似基态能量。

3. 屏蔽库伦势的应用

在《张朝阳的物理课》中，提到了屏蔽库伦势的概念，这是一种考虑电子间相互作用对库伦势影响的修正。在氦原子中，一个电子的存在会影响另一个电子感受到的核电荷，这种现象称为屏蔽效应。通过引入屏蔽因子，可以修正库伦势，使之更接近实际情况。

4. 变分法的具体步骤

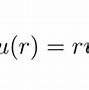
（1）选择试探波函数：通常选择斯莱特型（Slatertype）或高斯型（Gaussiantype）函数作为试探波函数，这些函数可以很好地描述电子云的分布。

（2）计算能量期望值：将试探波函数代入哈密顿量，计算能量期望值，并将其表示为试探波函数参数的函数。

（3）优化参数：通过数学方法（如梯度下降或共轭梯度法）优化试探波函数的参数，使得能量期望值最小。

（4）验证结果：将得到的基态能量与实验值或其他精确计算结果进行比较，验证变分法的准确性。

5. 结论

通过变分法结合屏蔽库伦势的应用，可以有效地计算氦原子基态能。这种方法不仅提供了理论计算的近似解，也为理解电子间相互作用提供了物理直觉。《张朝阳的物理课》中的屏蔽库伦势概念，为这一计算提供了理论基础，使得变分法在处理复杂量子系统时更加精确和有效。

通过上述分析，我们可以看到变分法在处理氦原子基态能问题上的强大能力，以及屏蔽库伦势在提高计算准确性方面的重要作用。这种方法的应用不仅限于氦原子，还可以扩展到其他多电子原子和分子系统，为量子化学和凝聚态物理的研究提供了有力的工具。