探索拉格朗日力学绕过传统受力分析的新途径

在传统的力学教学中，受力分析是解决问题的核心步骤。然而，这种方法往往复杂且容易出错，尤其是在处理多体问题或复杂系统时。《张朝阳的物理课》深入讲解了拉格朗日力学，这是一种可以绕过传统受力分析，更加高效和系统地解决力学问题的方法。

1. 拉格朗日力学简介

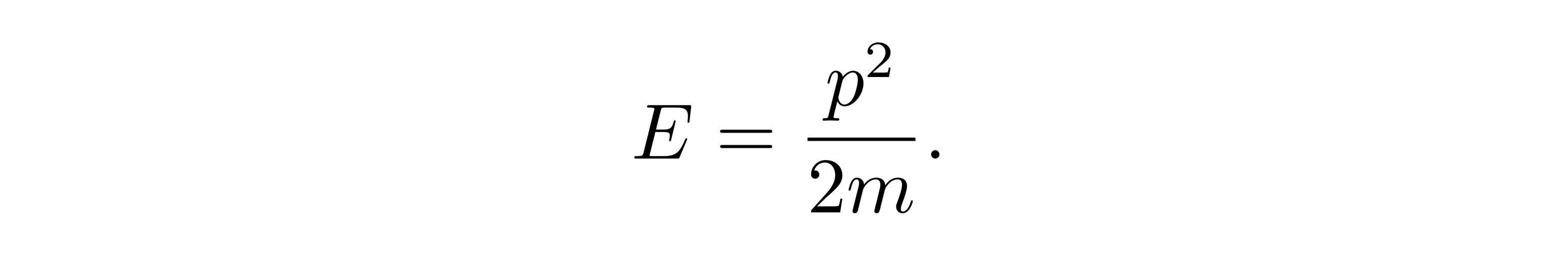
拉格朗日力学是由法国数学家约瑟夫·路易·拉格朗日于18世纪末发展起来的。它基于最小作用量原理，通过构建拉格朗日函数来描述系统的动力学行为。这种方法不直接分析每个物体的受力情况，而是通过系统的动能和势能来建立方程，从而简化了问题的处理。

2. 拉格朗日函数的构建

在拉格朗日力学中，一个系统的拉格朗日函数 \( L \) 定义为系统的动能 \( T \) 减去势能 \( V \)，即 \( L = T V \)。动能通常是速度的二次函数，而势能则依赖于系统的位置。通过选择合适的广义坐标，可以简化动能和势能的表达式，使得拉格朗日函数更加简洁。

3. 欧拉拉格朗日方程

拉格朗日力学的核心是欧拉拉格朗日方程，它是一个二阶微分方程，形式为 \( \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) \frac{\partial L}{\partial q_i} = 0 \)，其中 \( q_i \) 是广义坐标，\( \dot{q}_i \) 是其时间导数。这个方程自动包含了牛顿第二定律，但避免了直接的受力分析。

4. 应用实例

以《张朝阳的物理课》中的讲解为例，考虑一个简单的摆锤问题。在传统方法中，需要分析摆锤的重力和张力，并建立复杂的运动方程。而在拉格朗日力学中，只需定义摆锤的动能和势能，构建拉格朗日函数，然后应用欧拉拉格朗日方程即可得到摆锤的运动方程，大大简化了计算过程。

5. 拉格朗日力学的优势

拉格朗日力学的主要优势在于其普遍性和简洁性。它适用于任何保守系统，无论是平面的还是立体的，无论是简单的还是复杂的。通过选择合适的广义坐标，可以进一步简化问题，使得即使对于非惯性系或约束系统，也能轻松处理。

6. 结论

拉格朗日力学提供了一种强大的工具，用于绕过传统的受力分析，直接从系统的能量角度解决问题。这种方法不仅简化了计算，还提高了物理问题的处理效率。通过《张朝阳的物理课》的讲解，我们可以更深入地理解这一方法，并将其应用于更广泛的物理问题中。

通过这篇文章，我们不仅了解了拉格朗日力学的基本原理和应用，还体会到了它在现代物理学中的重要性和实用性。对于希望深入理解物理学和提高问题解决能力的读者来说，掌握拉格朗日力学无疑是一个宝贵的工具。