张朝阳的物理课解密张量与协变导数，探索时空弯曲的奥秘

在《张朝阳的物理课》中，张朝阳教授深入浅出地解释了如何描述时空的弯曲，这一概念在广义相对论中占据核心地位。时空弯曲是物质和能量存在的结果，它通过张量和协变导数这两个数学工具来精确描述。

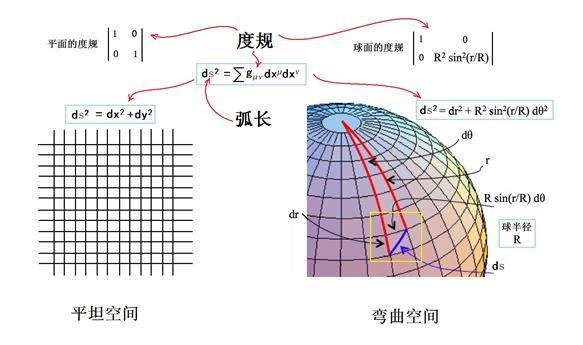
张量是一种多线性函数，它能够在不同的坐标系中保持其性质不变。在物理学中，张量被用来描述那些在坐标变换下不变的物理量，如应力、应变和电磁场强度等。在广义相对论中，时空的弯曲通过黎曼张量来描述，这是一个四阶张量，包含了时空曲率的所有信息。

协变导数是广义相对论中的一个重要概念，它用于描述在弯曲时空中矢量或张量的变化。与传统的偏导数不同，协变导数考虑了时空的曲率，因此能够准确地描述物体在弯曲时空中的运动轨迹。通过协变导数，我们可以计算出物体在时空中移动时，其速度和加速度的变化，从而理解引力如何影响物体的运动。

《张朝阳的物理课》通过讲解张量和协变导数，为我们提供了一个深入理解时空弯曲的框架。这些数学工具不仅帮助我们精确描述物理现象，揭示了宇宙的基本结构和运行机制。