```html
LQR控制编程介绍
线性二次调节(LQR)是一种经典的控制器设计方法,它通过最小化系统状态的加权和来设计控制器增益,以实现系统稳定性和性能优化. 在现代控制理论中被广泛应用。下面是LQR控制编程的一般步骤:
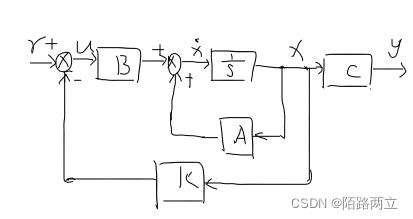
首先需要对要控制的系统进行数学建模,通常使用状态空间模型表示。这包括系统的状态方程和输出方程。状态方程描述了系统状态随时间的演变,输出方程描述了系统的输出与状态之间的关系。
LQR控制器的设计需要设定一个性能指标,通常是系统状态的加权和,表示为性能指标J。J可以是系统状态的加权二次型,也可以是其他性能指标。这一步骤主要是设定目标函数,也就是需要最小化的性能指标。
一旦系统建模和目标函数确定,就可以使用LQR控制器的设计方法来求解控制增益矩阵K。通常通过求解离散时间的Riccati方程或连续时间的代数Riccati方程来获得增益矩阵。
获得控制增益矩阵后,就可以将其应用于系统中,实现闭环控制。在实际编程中,需要将控制增益矩阵与状态反馈结合,实现对系统的控制。
需要对设计的控制器进行模拟和验证。通过对系统施加不同输入,观察系统的响应,并验证控制器的性能是否符合设计要求。如果需要,可以调整目标函数或重新设计控制器增益。
LQR控制编程需要对系统进行建模,设定目标函数,求解控制增益,实现控制器,并进行验证。这是一个对控制理论和编程技能都有要求的过程,但可以帮助实现系统的稳定控制和优化性能。
```
版权声明
本文仅代表作者观点,不代表百度立场。
本文系作者授权百度百家发表,未经许可,不得转载。











