牛顿迭代法（Newton's Method）是一种用于求解数值逼近的迭代方法。它可以通过不断逼近函数的根来解决方程或者优化问题。本文将对牛顿迭代法进行编程小结，包括算法原理、代码实现以及一些建议。

算法原理

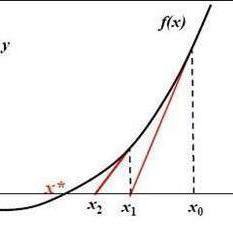
牛顿迭代法的算法原理是基于泰勒展开和切线的思想。假设我们要求解方程 $f(x) = 0$ 的根，可以通过选择一个初始点 $x_0$，然后不断迭代计算新的估计值 $x_{n 1}$，直到满足精度要求。具体的迭代公式如下：

$$x_{n 1} = x_n \frac{f(x_n)}{f'(x_n)}$$

其中，$f'(x)$ 表示函数 $f(x)$ 的导数。

代码实现

下面是使用 Python 语言实现牛顿迭代法的代码示例：

```python

def newton_method(f, df, x0, eps=1e6, max_iter=100):

x = x0

for _ in range(max_iter):

fx = f(x)

if abs(fx) < eps:

return x

dfx = df(x)

if dfx == 0:

break

x = fx / dfx

return None

```

其中，`f(x)` 和 `df(x)` 分别表示函数 $f(x)$ 和其导数 $f'(x)$ 的计算方式。`x0` 是初始点的取值。`eps` 表示迭代的精度要求，默认为 $10^{6}$。`max_iter` 是迭代的最大次数，默认为 100。

指导建议

在使用牛顿迭代法时，可以注意以下几点：

1. 选择合适的初始点：初始点的选择对牛顿迭代法的收敛性有影响。可以尝试不同的初始点，或者使用其他启发式方法来选择初始点。

2. 处理导数为零的情况：当迭代过程中导数为零时，迭代无法继续进行。可以在代码中添加对导数为零的判断，避免出现无法收敛的情况。

3. 控制迭代次数和精度：为了避免无限循环或计算过程过长，可以设置合适的最大迭代次数和精度要求。根据实际情况进行调整，以获得较好的计算效果。

4. 对特殊情况进行处理：牛顿迭代法可能出现振荡、发散或收敛到局部极值点的情况。可以根据具体问题进行特殊处理，比如添加阻尼系数或限制迭代范围。

牛顿迭代法是一种强大的数值计算方法，可以用于求解方程或优化问题。在实际应用中，需要根据具体情况进行适当的调整和处理，才能获得准确和稳定的结果。

牛顿迭代法编程小结

牛顿迭代法（Newton's Method）是一种用于求解数值逼近的迭代方法。

牛顿迭代法的算法原理是基于泰勒展开和切线的思想。

def newton_method(f, df, x0, eps=1e6, max_iter=100):
    x = x0
    for _ in range(max_iter):
        fx = f(x)
        if abs(fx) < eps:
            return x
        dfx = df(x)
        if dfx == 0:
            break
        x = fx / dfx
    return None